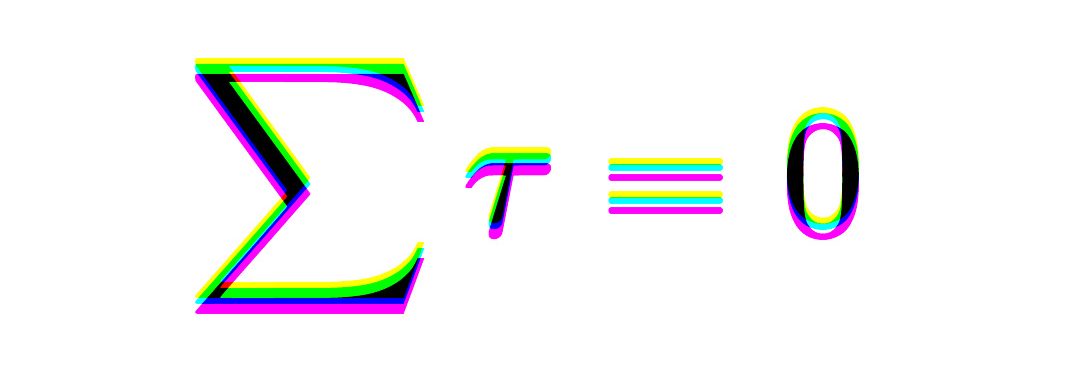A Unified Perspective on Newton’s Laws, Classical Forces, and the Fundamental Interactions

---

Abstract

A definition in modern day physics:
Torsion is a secondary mathematical property—either as a correction to curvature in spacetime, a mechanical response to applied torque, or a rarely considered effect in quantum field interactions—rather than as a fundamental principle governing all forces, motion, and energy.

Torsion Redefined:
Torsion is the primary mechanism underlying all forces and interactions in nature. Rather than being a secondary effect, I propose that torsion is the fundamental cause of all motion, structure, and energy exchange—from quantum particles to cosmic-scale phenomena.

Torsion manifests in multiple forms:

1. Linear Torsion (τ_L) – Torsional stress propagating in a straight line, observed in forces like tension, compression, and shear.
2. Radial or Rotational Torsion (τ_R) – The twisting of spacetime or matter, leading to rotation, vorticity, and angular momentum conservation.
3. Helical & Supercoiling Torsion (τ_S) – When torsion accumulates in a closed-loop system, it redistributes itself by forming supercoils, minimizing energy expenditure while conserving torsional balance.

Mathematically, torsion is expressed as:

   

which asserts that torsion is always conserved and governs the balance of forces across all scales aligning with Newton’s third law which states – For every action, there is an equal and opposite reaction.

Thus: If one part of a system twists, compresses, or accelerates, another part must counteract, expand, or release energy.

Physics describes four fundamental forces:

• Gravity,
• Electromagnetism,
• Strong Force,
• Weak Force.

While these forces appear distinct, they share common structural features that suggest a deeper underlying principle.

I propose that:

• Gravity is the result of large-scale torsional density gradients in spacetime.
• Electromagnetism emerges from propagating torsional waves.
• The Strong Force is a manifestation of quark confinement through supercoiled torsion.
• The Weak Force is the result of rearranging internal torsion states in particles.

From fundamental particles to DNA helices, vortex rings, and galactic structures, torsion governs the organization of matter and energy across all scales. This paper introduces a rigorous definition of torsion, presents evidence of its universality, and explores its implications for unifying physical laws.

---

Introduction

Many phenomena such as particle interactions, fluid dynamics, and cosmic evolution—exhibit torsional behaviours, yet torsion remains an overlooked component in fundamental physics. For example, neither General Relativity nor Einstein-Cartan theory properly account for torsion in their formulas. Unfortunately many modern day physics are based on those formulas.

General Relativity (GR)

GR models spacetime as a purely curved manifold without torsion. However, in systems with angular momentum or intrinsic spin, torsion effects cannot be neglected.

Einstein-Cartan Theory (EC)

EC theory remains incomplete because it only accounts for external torsion—torsional effects that arise from the motion of objects through spacetime. It does not include internal torsion, which affects mass-energy at the subatomic level.

---

If we take a torsion-first approach, I propose that all forces arise as manifestations of torsion—the twisting, coiling, and redistribution of energy in spacetime and matter.

My Goal

My goal is to redefine torsion as the foundational principle behind all forces and interactions. Rather than treating torsion as a secondary effect of motion, I propose that torsion is the cause of all motion. This approach provides a framework that unifies classical mechanics, quantum mechanics, and relativity under a single, coherent principle.

Key questions we will address:

1. What is torsion, and how do we define it mathematically?
2. How does torsion manifest at different scales, from quantum particles to cosmic structures?
3. Can all forces in nature be described as emergent properties of torsion?

By answering these questions, I aim to establish torsion as the unifying principle of physics.

---

1. Defining Torsion

Conceptual Definition

Torsion is the fundamental tendency of a system to twist, supercoil, or redistribute stress to maintain balance. It is not simply “twist”; rather, it is the underlying property governing how forces distribute across spacetime and matter.

Mathematical Definition

Torsion can be represented in multiple ways depending on context:

1. Torsion Balance Equation (General Form):

      

   This equation states that sum (∑) of all torsion (τ) must always balance within a system—an increase in one region must be compensated by a decrease elsewhere. This principle ensures that energy and motion are conserved in a system, and that any localized increase in torsional stress must be counteracted by a corresponding release elsewhere. This corresponds with Newton’s third law—For every action, there is an equal and opposite reaction.
   
2. Torsion and Angular Motion:

      

   
   This equation describes how torsion relates to rotational motion. Here, τ (tau) represents the total torsional force, I is the torsional moment of inertia (analogous to mass in linear motion), and α (alpha) is the angular acceleration. This states that an applied torsional force will cause an angular acceleration proportional to the system’s torsional inertia, just as Newton’s second law describes linear motion.
   
3. Torsion and Energy Storage (Supercoiling Model):

      

   
   This equation expresses how torsion stores energy. Here, E represents the stored torsional energy, I is the torsional moment of inertia, and ω is the rotational velocity. This states that torsional systems accumulate and store energy in rotational motion, much like how linear motion stores kinetic energy. Systems exhibiting supercoiling, such as DNA and vortex rings, optimize energy retention by redistributing torsion into more stable configurations.

These definitions provide a framework for understanding how torsion drives motion, stores energy, and governs interactions across all scales.

---

2. Redefining Mass, Energy, and Force in a Torsion-First Framework

A. Mass as Torsional Inertia

• Traditional View: Mass is an intrinsic property of matter that resists acceleration.
• Torsion-First View: Mass arises from torsional inertia, the resistance of a system to changes in its torsional state.

     

  where I is the torsional moment of inertia.
• Implication: Particles with greater internal torsional complexity have higher mass.
  • Quarks bound in protons/neutrons → Mass emerges from torsional supercoiling.
  • Higgs mechanism as torsional resistance → Mass arises from interactions within the torsion field.

B. Energy as Stored Torsion

• Traditional View: Energy is the ability to do work, existing in kinetic, potential, and other forms.
• Torsion-First View: Energy is the capacity of a system to store and redistribute torsional stress.

     

  where ω represents intrinsic torsional oscillation.
• Implication:
  • Rest energy (E=mc²) → Represents a perfectly balanced torsional state at equilibrium.
  • Kinetic energy → Motion is a propagation of torsion rather than a separate concept.
  • Potential energy → Arises from torsional constraints, as in DNA supercoiling or elastic deformation.

C. Force as Torsional Redistribution

• Traditional View: Force is an interaction that changes an object’s momentum.
• Torsion-First View: Force is the redistribution of torsion between regions of different torsional density.

     

  • Compression, tension, and shear → All result from torsional redistribution.
  • Electromagnetic forces → Emerge as torsional wave propagation rather than field interactions.
  • Gravitational attraction → Arises from torsional energy density gradients in spacetime.

Since torsion must always balance (∑τ=0), mass, energy, and force are not separate concepts but different manifestations of torsion conservation.

---

3. Newton’s Laws in a Torsion-First Framework

Newton’s Second Law:
Force as a Torsional Effect

Newton’s second law is typically written as:

   

where force (F) is the product of mass (m) and acceleration (a).

However, in a torsion-first view, force is simply the redistribution of torsion in a system. Instead of viewing motion as linear, we define:

   

where:

• τ is the torsional force (analogous to Newton’s force but applied in rotational/spatial torsion).
• I is the torsional inertia (resistance to twisting, akin to mass in Newton’s second law).
• α is the torsional acceleration (how fast the system is twisting).

Analogy: When you spin a fidget spinner, it resists changes in motion due to torsional inertia—this is the rotational counterpart of Newton’s second law.

Thus, Newton’s second law is just a special case of torsion applied to linear acceleration.

If we take a torsion-first approach, then energy (E) itself must be defined in terms of torsion. That means equations should not introduce energy as an independent variable, but rather derive it directly from torsion.

---

Newton’s Third Law:
Action-Reaction as Torsion Balance

Newton’s Third Law states:

   

This is naturally explained by torsion conservation:

• Compress one part of a system, and another part expands.
• Twist an object, and an opposite counter-twist develops.
• Increase the energy in one region, and it must dissipate or be stored elsewhere (as supercoiling).

Analogy: If you squeeze one end of a water balloon, the water redistributes to balance the pressure—this is torsion balancing itself.

---

4. Reformulating Energy in Terms of Torsion

Energy is typically defined as:

   

where force (F) acts over a distance (d).
But since force is just a redistribution of torsion, we need a torsional definition of energy.

A natural analogy is rotational kinetic energy:

   

where:

• I is the moment of inertia (torsional resistance).
• ω is the angular velocity.

Since we already define torsion (τ) as:

   

and since angular acceleration is the derivative of velocity (α=dω/dt), we can rewrite energy as:

   

where:

• θ represents the torsional displacement (the total twist applied).
• τ represents the torsional force (how much twisting occurs).

Thus, energy is not an independent quantity—it emerges from the torsion stored in a system.

---

5. Updating the Fundamental Equation

Since energy is already encoded in torsion, our equation:

   

should instead be rewritten fully in terms of torsion:

   

or, in the most general case:

   

This equation states that torsion is always conserved, but it can transfer between different forms, such as rotational energy or supercoiling states.

---

6. What This Means for the Theory of Everything

• Mass is stored torsion.
• Energy is the dynamic form of torsion interacting with space.
• All forces are just ways torsion is redistributed in a system.
• Supercoiling is nature’s way of minimizing energy by stabilizing torsion.
• When external energy (torsion) is added, the system must release or store it in a new configuration.

These equations could fully replace the classical definitions of force, mass, and energy—everything becomes a torsional exchange.

---

7. Common Forces in Everyday Life Explained by Torsion

Let’s break down common mechanical forces using the torsion-first principle.

A. Compression & Expansion: The Torsion of Pressure

• When you press down on a spring, it resists by trying to expand back.
• This is because compressing a system increases local torsion density.
• The system reacts by trying to release that torsion via expansion.

Example: Squeezing a stress ball—your fingers apply torsion inward, and the ball reacts outward to restore balance.

---

B. Tension: Linear Torsion Trying to Unwind

• When you stretch a rubber band, you’re adding linear torsion.
• If you let go, it releases stored torsional energy by snapping back to its lower-energy state.

Example: Tug-of-war—each team applies opposing torsional tension, and the rope distributes the stress.

---

C. Shear: Opposing Torsion on Different Layers

• Shear forces occur when different parts of a system experience torsion in opposite directions.
• This happens in cutting, tearing, or frictional forces.

Example: When you rub your hands together, you create shear torsion—heat emerges as energy dissipates.

---

8. The Fundamental Forces as Torsional Effects

Now, let’s extend this principle to the four fundamental forces.

A. Gravity as a Torsional Curvature of Spacetime

• Instead of viewing gravity as pure curvature, we see it as torsion density in spacetime.
• More mass = higher torsion, pulling nearby objects into lower-energy torsional states.
• Supercoiled spacetime structures, such as black holes, trap torsion, preventing escape.

Analogy: Think of a whirlpool—water (spacetime) twists inward, pulling objects toward the center.

---

B. Electromagnetism as Torsional Wave Propagation

• Electric fields arise from torsional dipoles (positive and negative charges as opposite torsion modes).
• Magnetic fields emerge from twisting electric charge flow, creating torsional loops in spacetime.

Analogy: Think of a stretched slinky—apply a twist at one end, and the wave propagates through the coils.

---

C. Strong Force: Supercoiled Torsion Locking Quarks Together

• Quarks are confined within nucleons due to torsional supercoiling.
• Separating quarks increases torsion, requiring immense energy to break the bond.
• Gluons are not force carriers—they are torsional energy modes stabilizing the system.

Analogy: Twisting multiple rubber bands together creates a supercoiled structure—the more twisted, the stronger the bond.

---

D. Weak Force: Torsional Chirality Flips

• Weak interactions involve torsional realignments of particles.
• This explains why the weak force affects chirality (left-handed vs. right-handed particle states).
• Weak decay may be a torsion imbalance correcting itself by flipping particle states.

Analogy: A spinning coin that suddenly flips over—a chirality transition triggered by instability.

---

9. Conclusion: A Torsion-Based Theory of Everything?

By generalizing all forces using torsion-first principles, we unify classical mechanics and fundamental interactions under one simple rule:

   

This means:

• All forces are manifestations of torsion balancing itself.
• Stable structures emerge from supercoiling, where torsion minimizes energy.
• External energy can break this balance, causing chain reactions or transformations.

Final Analogy: The universe is like a giant tangled slinky—every force is just a different way torsion propagates, builds up, or unwinds.